Some math problems that I don't have a good solution for

I recently realized that I was having a lot of math problems that I couldn't find a good way to solve, so I thought I might as well write them down and share them online. All these are for personal projects of mine, nothing huge or industry-shaking.

If you have good info, or straight-up solutions, feel very free to contact me via email! Alternatively, maybe they can serve as fun excercises if you're bored. If I solve any, I'll mark them as solved, and share my findings.

A very specific Quartic Equation
An analytical 2D fourier transform of a simple shape - Solved!
A Method for simulating aerodynamics at orbital velocities and low density gasses

A very specific Quartic Equation

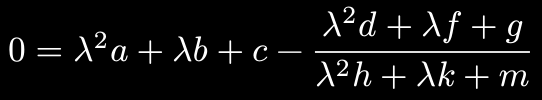
0 = lambda^2 a + lambda b + c - (lambda^2 d + lambda f + g)/(lambda^2 h + lambda k + m) — The equation in question

The goal is a basic formula/program to solve for the smallest real and positive lambda. All other variables in the equation are known, real and positive. The context is a simple program on the gpu that has to solve this equation in parallel for many datapoints.

It can be rewritten into a more obviously quartic equation like so (keeping in mind that lambda^2 h + lambda k + m != 0):

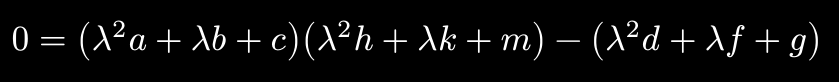
0 = (lambda^2 a + lambda b + c)*(lambda^2 h + lambda k + m) - lambda^2 d + lambda f + g — Quartic formulation

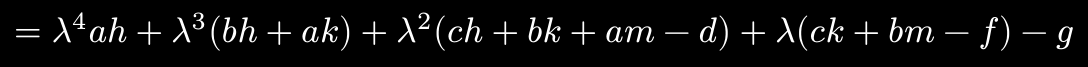
0 = lambda^4 ah + lambda^3 (bh + ak) + lambda^2 (ch + bk + am - d) + lambda (ck + bm - f) - g — Quartic formulation

And a formula for solving quartic equations does exist, but:

It has multiple solutions, of which I want only 1 specific one.
It is computationally expensive, with complex (as in real-imaginairy) arithmetic and a lot of square roots.
It is made to solve the most general case of the equation, which is not this case, mine has a lot of constraints.

Right now, I'm planning to solve this by doing a basic good guess, and doing some iteration based on the derivative of the function.

An analytical 2D fourier transform of a simple shape - Solved!

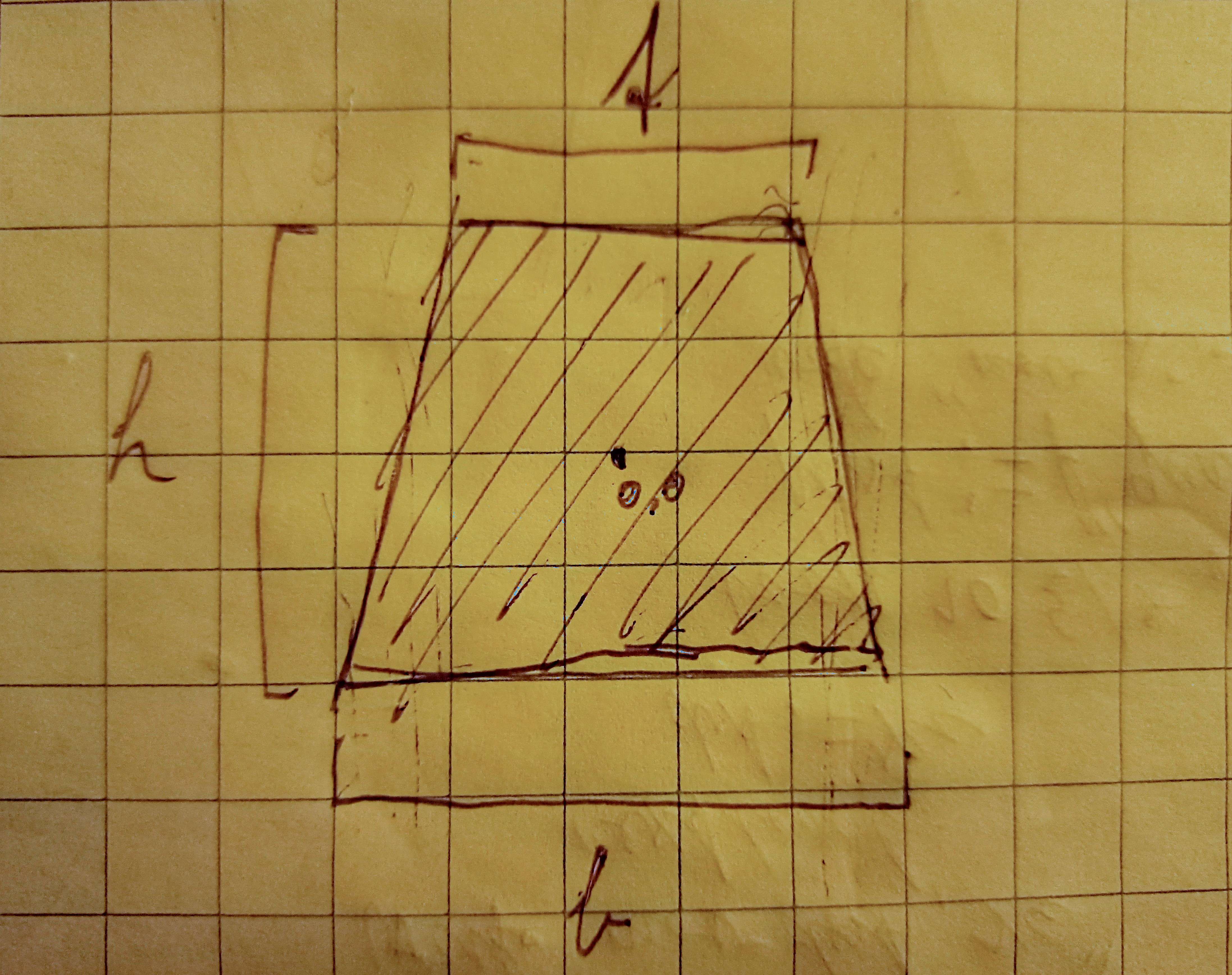
The shape in question. The origin is in the middle, the shaded area is 1, the rest is 0.

This one is a little bit emberassing, but it's been a while since I've done a proper 2D integral, and I do not have a good intuition for how I should go about it.

With some help from friends and Wolfram Alpha, I finally got this one. It turned out to be quite a complicated integral, so it might be a while before I translate it all to LaTeX.

A Method for simulating aerodynamics at orbital velocities and low density gasses

Any discussion on fluid simulation must acknowledge that solving the Navier Stokes Equations is really difficult, hypersonic flow (and above) especially so. That being said, I suspect that there are some good approximations you can make with a really low density (very upper atmosphere) and weakly self-interacting gas. The question is mostly how far those approximations apply.

I haven't done a perfect problem formulation for this yet, but I will eventually update this with specific velocities and densities.